Conquering Challenging Sine Graphs: Transformation Practice Problems
Sine graphs, with their rhythmic undulations, are fundamental to understanding periodic phenomena in mathematics, physics, and engineering. However, transforming these graphs can present a significant challenge for students. This article delves into tackling challenging sine graphs transformations practice problems, providing a comprehensive guide to mastering these complex concepts. We’ll explore various transformation types, offer step-by-step solutions, and equip you with the skills to confidently navigate even the most intricate sine wave manipulations. Whether you’re a student preparing for an exam or a professional seeking a refresher, this guide offers valuable insights into the world of sine graph transformations.
Understanding the Basics: The Parent Sine Function
Before diving into transformations, it’s crucial to have a firm grasp of the parent sine function, y = sin(x). This function serves as the foundation for all subsequent transformations. Key characteristics of the parent sine function include:
- Amplitude: The amplitude is the maximum displacement of the graph from its midline (the x-axis in this case). For y = sin(x), the amplitude is 1.
- Period: The period is the length of one complete cycle of the sine wave. For y = sin(x), the period is 2π.
- Phase Shift: The phase shift is the horizontal displacement of the graph. For y = sin(x), the phase shift is 0.
- Vertical Shift: The vertical shift is the vertical displacement of the graph. For y = sin(x), the vertical shift is 0.
Types of Sine Graph Transformations
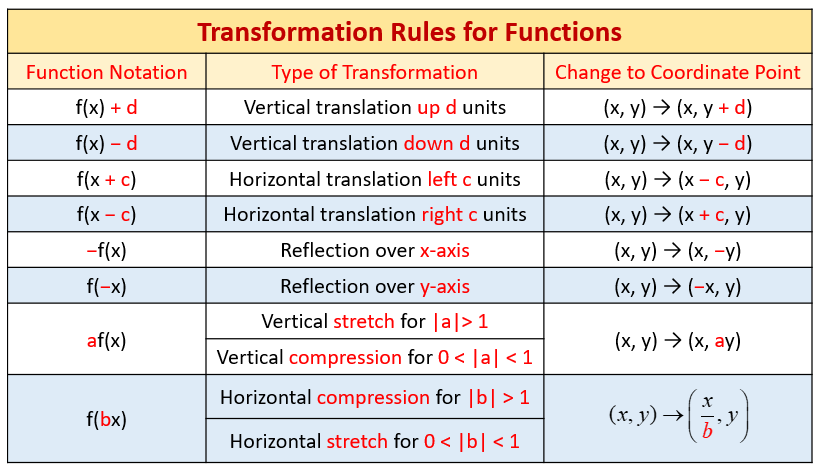
Transformations alter the shape and position of the parent sine function. Common types of transformations include:
Vertical Stretches and Compressions
A vertical stretch or compression is represented by the equation y = A sin(x), where A is a constant. If |A| > 1, the graph is stretched vertically by a factor of A. If 0 < |A| < 1, the graph is compressed vertically by a factor of A. The amplitude of the transformed graph is |A|.
Example: y = 3 sin(x) stretches the parent sine function vertically by a factor of 3, resulting in an amplitude of 3. y = 0.5 sin(x) compresses the parent sine function vertically by a factor of 0.5, resulting in an amplitude of 0.5.
Horizontal Stretches and Compressions
A horizontal stretch or compression is represented by the equation y = sin(Bx), where B is a constant. If |B| > 1, the graph is compressed horizontally by a factor of B. If 0 < |B| < 1, the graph is stretched horizontally by a factor of B. The period of the transformed graph is 2π/|B|.
Example: y = sin(2x) compresses the parent sine function horizontally by a factor of 2, resulting in a period of π. y = sin(0.5x) stretches the parent sine function horizontally by a factor of 2, resulting in a period of 4π.
Phase Shifts (Horizontal Translations)
A phase shift is represented by the equation y = sin(x – C), where C is a constant. If C > 0, the graph is shifted horizontally to the right by C units. If C < 0, the graph is shifted horizontally to the left by |C| units.
Example: y = sin(x – π/2) shifts the parent sine function horizontally to the right by π/2 units. y = sin(x + π/4) shifts the parent sine function horizontally to the left by π/4 units.
Vertical Shifts (Vertical Translations)
A vertical shift is represented by the equation y = sin(x) + D, where D is a constant. If D > 0, the graph is shifted vertically upward by D units. If D < 0, the graph is shifted vertically downward by |D| units. The midline of the transformed graph is y = D.
Example: y = sin(x) + 2 shifts the parent sine function vertically upward by 2 units. y = sin(x) – 1 shifts the parent sine function vertically downward by 1 unit.
Reflections
Reflections can occur across the x-axis or the y-axis. A reflection across the x-axis is represented by the equation y = -sin(x). A reflection across the y-axis is represented by the equation y = sin(-x), which is equivalent to y = -sin(x) due to the odd symmetry of the sine function.
Solving Challenging Sine Graphs Transformations Practice Problems
Now, let’s tackle some challenging sine graphs transformations practice problems. We’ll break down each problem step-by-step to illustrate the application of the concepts discussed above.
Problem 1: Graphing y = 2sin(x – π/3) + 1
This equation combines multiple transformations. Let’s analyze each one:
- Vertical Stretch: The coefficient 2 indicates a vertical stretch by a factor of 2, resulting in an amplitude of 2.
- Phase Shift: The term (x – π/3) indicates a phase shift to the right by π/3 units.
- Vertical Shift: The constant +1 indicates a vertical shift upward by 1 unit.
To graph this function, follow these steps:
- Start with the parent sine function, y = sin(x).
- Apply the vertical stretch: Multiply the y-values of the parent function by 2 to obtain y = 2sin(x).
- Apply the phase shift: Shift the graph of y = 2sin(x) to the right by π/3 units to obtain y = 2sin(x – π/3).
- Apply the vertical shift: Shift the graph of y = 2sin(x – π/3) upward by 1 unit to obtain y = 2sin(x – π/3) + 1.
The resulting graph has an amplitude of 2, a period of 2π, a phase shift of π/3 to the right, and a midline of y = 1.
Problem 2: Graphing y = -sin(2x) – 0.5
This equation also involves multiple transformations:
- Reflection: The negative sign in front of the sine function indicates a reflection across the x-axis.
- Horizontal Compression: The coefficient 2 inside the sine function indicates a horizontal compression by a factor of 2, resulting in a period of π.
- Vertical Shift: The constant -0.5 indicates a vertical shift downward by 0.5 units.
To graph this function, follow these steps:
- Start with the parent sine function, y = sin(x).
- Apply the reflection: Reflect the graph of y = sin(x) across the x-axis to obtain y = -sin(x).
- Apply the horizontal compression: Compress the graph of y = -sin(x) horizontally by a factor of 2 to obtain y = -sin(2x).
- Apply the vertical shift: Shift the graph of y = -sin(2x) downward by 0.5 units to obtain y = -sin(2x) – 0.5.
The resulting graph has an amplitude of 1, a period of π, no phase shift, and a midline of y = -0.5. The reflection across the x-axis inverts the typical sine wave pattern.
Problem 3: Determining the Equation from a Graph
This type of challenging sine graphs transformations practice problems requires you to analyze a given graph and determine the equation that represents it. Look for the following key features:
- Amplitude: Measure the distance from the midline to the maximum or minimum point of the graph.
- Period: Measure the length of one complete cycle of the wave. Use this to calculate the value of B in the equation y = sin(Bx) or y = cos(Bx). Remember Period = 2π/|B|.
- Phase Shift: Determine how far the graph has been shifted horizontally compared to the parent sine or cosine function. Note if a sine or cosine function is a better fit after the phase shift.
- Vertical Shift: Identify the midline of the graph. This will be the value of D in the equation y = sin(x) + D.
- Reflection: Determine if the graph is reflected across the x-axis. If so, the equation will have a negative sign in front of the sine or cosine function.
For example, if a graph has an amplitude of 3, a period of π, a phase shift of π/4 to the left, and a midline of y = 2, the equation would be y = 3sin(2(x + π/4)) + 2. Or equivalently, y = 3sin(2x + π/2) + 2.
Tips for Mastering Sine Graph Transformations
Mastering sine graph transformations requires practice and a solid understanding of the underlying concepts. Here are some helpful tips:
- Practice Regularly: The more you practice, the more comfortable you’ll become with identifying and applying transformations.
- Use Graphing Tools: Graphing calculators or online graphing tools can help you visualize the effects of different transformations. Desmos and GeoGebra are excellent resources.
- Break Down Complex Transformations: When faced with multiple transformations, break them down into smaller, more manageable steps.
- Understand the Relationship Between Equations and Graphs: Focus on connecting the equation of a transformed sine function to its graphical representation.
- Review Trigonometric Identities: A strong understanding of trigonometric identities can simplify complex expressions and make transformations easier to understand.
- Focus on Key Points: Pay attention to key points such as the maximum, minimum, intercepts, and midline. These points can help you quickly sketch the graph and identify transformations.
Common Mistakes to Avoid
When working with sine graph transformations, it’s important to be aware of common mistakes:
- Incorrectly Applying Phase Shifts: Remember that the phase shift is determined by the term (x – C), not just C. A positive C shifts the graph to the *right*, not the left.
- Confusing Horizontal and Vertical Transformations: Pay close attention to whether a transformation affects the x-axis (horizontal) or the y-axis (vertical).
- Forgetting the Order of Operations: Apply transformations in the correct order. Generally, stretches/compressions and reflections should be applied before shifts.
- Misinterpreting the Amplitude: The amplitude is always a positive value. If the graph is reflected across the x-axis, the amplitude is still the distance from the midline to the maximum or minimum point.
- Not Checking Your Work: Always double-check your graph to ensure it matches the equation and that all transformations have been applied correctly.
Advanced Concepts and Further Exploration
Once you’ve mastered the basics of sine graph transformations, you can explore more advanced concepts, such as:
- Damped Sine Waves: Sine waves with decreasing amplitude over time.
- Fourier Series: Representing complex periodic functions as a sum of sine and cosine waves.
- Applications in Physics and Engineering: Understanding how sine waves are used to model sound waves, light waves, and electrical signals.
By tackling challenging sine graphs transformations practice problems and understanding the underlying principles, you can develop a strong foundation in trigonometry and its applications. Remember to practice consistently, utilize graphing tools, and break down complex problems into smaller steps. With dedication and perseverance, you can confidently conquer even the most intricate sine wave manipulations. Good luck!
Understanding challenging sine graphs transformations practice problems is a key skill for anyone studying trigonometry or calculus. Practicing these problems will help you solidify your understanding of the concepts and improve your problem-solving abilities. Keep practicing and you’ll become proficient in transforming sine graphs in no time! Look for more challenging sine graphs transformations practice problems online or in textbooks. Remember to carefully analyze the equation before attempting to graph it. Many resources provide worked examples of challenging sine graphs transformations practice problems.
Consider exploring resources that offer challenging sine graphs transformations practice problems with detailed solutions. This can be invaluable for understanding the nuances of each transformation. Also, remember the core concepts when tackling challenging sine graphs transformations practice problems.
Ultimately, mastering challenging sine graphs transformations practice problems involves a combination of theoretical understanding and practical application. Keep practicing, and you’ll find yourself becoming more and more confident in your ability to work with sine graphs and their transformations. Keep seeking out those challenging sine graphs transformations practice problems!
[See also: Graphing Trigonometric Functions]
[See also: Understanding Amplitude and Period]
[See also: Phase Shift Explained]
